This action will delete this post on this instance and on all federated instances, and it cannot be undone. Are you certain you want to delete this post?
toddsundsted@epiktistes.comBetter dead than bored.
| Introduction | https://epiktistes.com/introduction |
|---|---|
| GitHub | https://github.com/toddsundsted/ktistec |
| Pronouns | he/him |
| 🌎 | Sector 001 |

I've streamlined theme development in Ktistec. The theming system uses a hierarchy of CSS custom properties and fallbacks. Theme authors can customize a theme at multiple levels:
Base Colors Only
Define only base colors like --text-primary, --bg-primary, --bg-input, --semantic-primary, etc. Derived colors will auto-generate using color-mix formulas. For example:
:root { --semantic-primary: #ffa500; }From this one line, theme-appropriate colors like --bg-accent-code, --anchor-color, etc. auto-generate.
Base Colors Plus Derived Colors
Define base colors and derived colors. Derived colors use custom values when defined. Undefined derived colors auto-generate. For example:
:root {
--text-primary: #333;
--text-primary-2: #ff0000; /* red for this specific shade */
}Given this theme, derived shades like --text-primary-1, --text-primary-3, and --text-primary-4 auto-generate. --text-primary-2 is red.
The simplest possible interesting theme redefines the primary semantic color. The single line above (in Base Colors Only) would result in the following, with button color, link color, disabled, selected, and hover states all derived automatically:
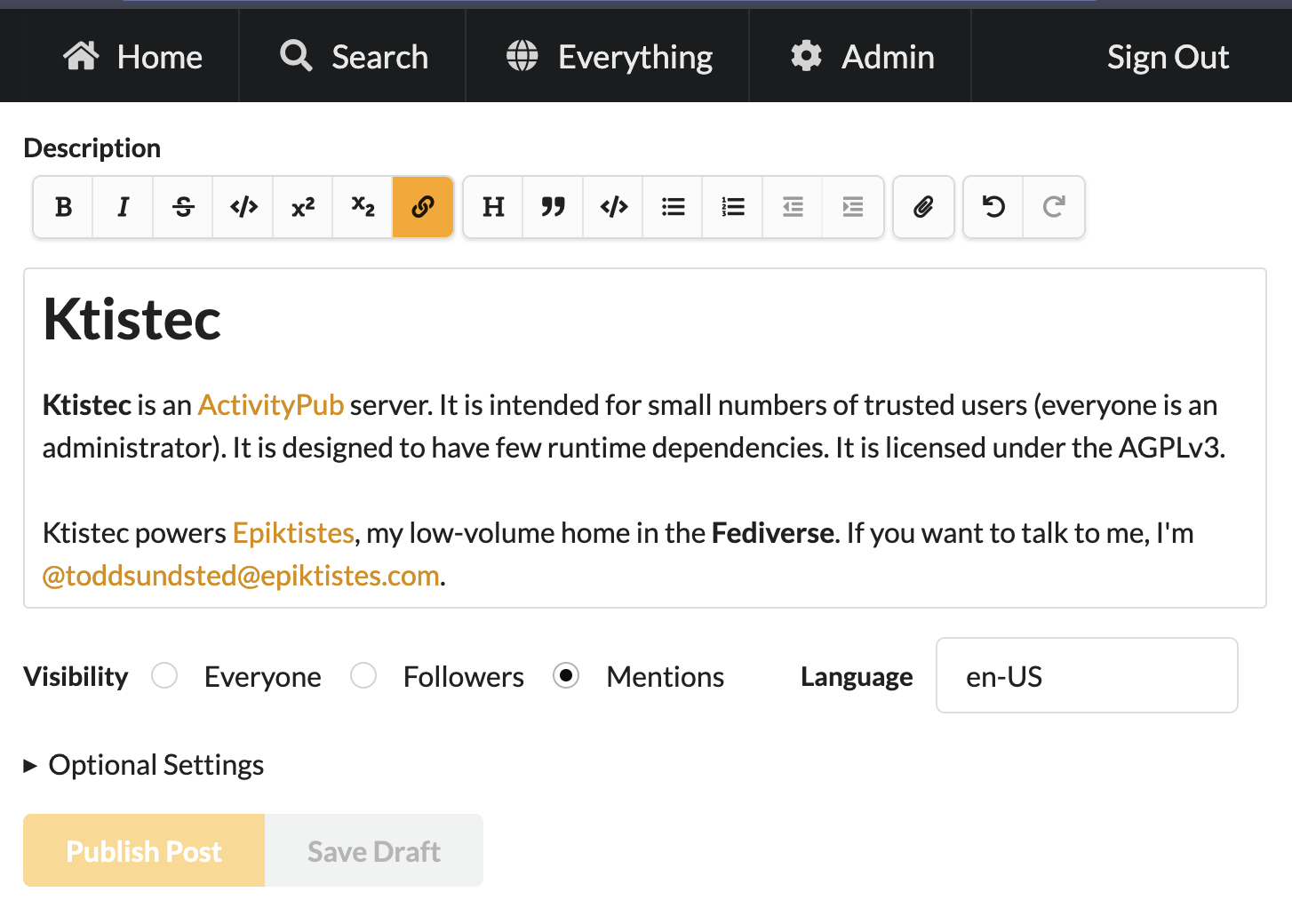
These changes will be in the upcoming release. Existing themes will continue to work, as is.

Experimenting with x-ray mode for ktistec.

Release v3.2.1 of Ktistec adds support for bookmarking posts. This was so immediately useful I don't know why it took me so long to get around to it!
Pinned/featured posts are in the works for the next release.
The full changelog:
Added
- Support for bookmarking posts.
Fixed
- Invalidate user's sessions after changing password.
- Ignore supplied languages that don't conform to expected format.
Changed
- Upgrade Kemal.
In other thoughts... I'd like to make followed hashtags more consumable. I follow ~10 hashtags and: 1) it's hard to tell what's new, 2) it feels like they arrive in large batches that are difficult to digest, and 3) the reading experience is meh.

I just discovered Pirate Weather.

It’s never the compiler or standard library.
It’s never the compiler or standard library.
Sometimes it’s the standard library…

commits b9e0658d to d42482bb cut the time required to run all #ktistec tests from ~35 seconds to ~26 seconds, a savings of about 25% (there are currently 5114 tests). the faster tests run, the more you run them, so this is a good outcome.

emacs comes with dunnet. i've never played it. today i am going to play it.

no #ktistec release this week. i have been working on bookmarked posts, pinned/featured posts, as well as some minor performance improvements, but i need to spend time fixing an issue with my libxml extensions that is preventing me from moving to the latest release of #crystallang. i've been putting it off but it's gotta get done, so...

My post on using emoji in Crystal Language identifiers got some 🎉 attention. The obvious question was, how much further could I take a Crystal based solution? I played around with macros for a while to see how much syntax I could replace, but that path didn't go very far. Too much of the language, like block delimiters, showed through.
It turns out there is at least one programming language designed almost entirely around emoji—Emojicode. Emojicode is pretty cool and impressively complete, but because Emojicode is, at its core, a fairly traditional imperative language, it is difficult to keep the ASCII out. 🤔
I thought I could do better by modeling an emoji-based programming language on a stack-based language like Forth. 💡 Heavy use of recursion and the stack makes it easy to avoid naming things, which means ✨ less ASCII and more emoji ✨.
This ugly duckling defines a word (a function) that computes a factorial. The factorial word is the character ❗ (the syntax 📖❗ ... 📕 defines it as a new word). You can see that ❗ calls itself recursively, right?
💭 Factorial 📖❗📚2️⃣⬇️❓👍🗑️1️⃣👎📚1️⃣➖❗✖️🔚📕 🔢5❗😀 💭 120 🔢10❗😀 💭 3628800
You can use spaces and line breaks to make things more readable, but a lot of Forth code kind of looks like this to me so 🤷.
There's already a small number of primitive words and a standard library of additional words. I'll probably play around with the core a bit more and then publish it.
Tower of Hanoi 🏯 works, too!

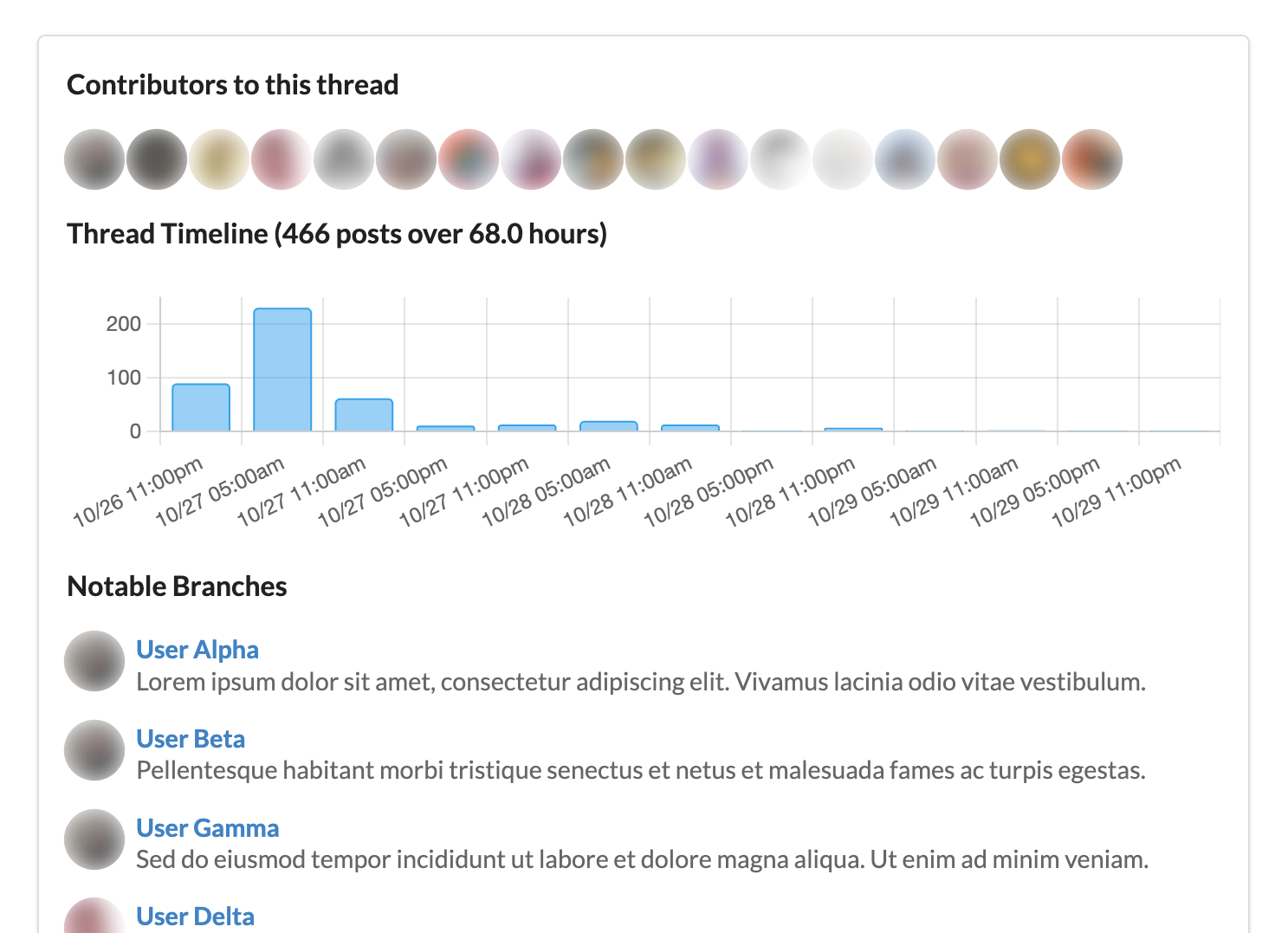
The major feature in v3.2.0 of Ktistec is thread analysis. The previous release, v3.1.2, added support for viewing threads from Lemmy communities. I follow the Open Source community, which leads to many large threads. The thread on FFMpeg and Google has 112 posts and is still growing.
Thread analysis helps me navigate these extensive conversations. It includes: top contributors, a timeline histogram, and notable branches.
The analysis applies several heuristics to identify interesting branches of the main thread. “Interesting” is subjective, but the algorithm currently looks for sudden bursts of activity and highlights those areas. Ktistec uses this to create a table of contents that links directly to those branches. Clicking on one of these links takes you to a branch-only view that focuses on the selected part of the thread.
It's fast—I anticipated needing to cache analyses, but analyzing a thread with over 400 posts takes only about 50 milliseconds on my production server.
This release also addresses an object visibility regression that was introduced in a previous version.
Full Changelog
Added
- Thread analysis that displays key participants, a timeline histogram, and notable branches
- New MCP tools:
analyze_threadandget_thread - Focal point rendering support for image attachments
Fixed
- Regression in object visibility affecting replies to threads
Changed
- Enhanced MCP tool details for likes, dislikes, and announces
- Improved cookie security.